Zippers

While Haskell's purity comes with a whole bunch of benefits, it makes us tackle some problems differently than we would in impure languages. Because of referential transparency, one value is as good as another in Haskell if it represents the same thing.

So if we have a tree full of fives (high-fives, maybe?) and we want to change one of them into a six, we have to have some way of knowing exactly which five in our tree we want to change. We have to know where it is in our tree. In impure languages, we could just note where in our memory the five is located and change that. But in Haskell, one five is as good as another, so we can't discriminate based on where in our memory they are. We also can't really change anything; when we say that we change a tree, we actually mean that we take a tree and return a new one that's similar to the original tree, but slightly different.

One thing we can do is to remember a path from the root of the tree to the element that we want to change. We could say, take this tree, go left, go right and then left again and change the element that's there. While this works, it can be inefficient. If we want to later change an element that's near the element that we previously changed, we have to walk all the way from the root of the tree to our element again!

In this chapter, we'll see how we can take some data structure and focus on a part of it in a way that makes changing its elements easy and walking around it efficient. Nice!

Taking a walk

Like we've learned in biology class, there are many different kinds of trees, so let's pick a seed that we will use to plant ours. Here it is:

data Tree a = Empty | Node a (Tree a) (Tree a) deriving (Show)

So our tree is either empty or it's a node that has an element and two subtrees. Here's a fine example of such a tree, which I give to you, the reader, for free!

freeTree :: Tree Char
freeTree =
    Node 'P'
        (Node 'O'
            (Node 'L'
                (Node 'N' Empty Empty)
                (Node 'T' Empty Empty)
            )
            (Node 'Y'
                (Node 'S' Empty Empty)
                (Node 'A' Empty Empty)
            )
        )
        (Node 'L'
            (Node 'W'
                (Node 'C' Empty Empty)
                (Node 'R' Empty Empty)
            )
            (Node 'A'
                (Node 'A' Empty Empty)
                (Node 'C' Empty Empty)
            )
        )

And here's this tree represented graphically:

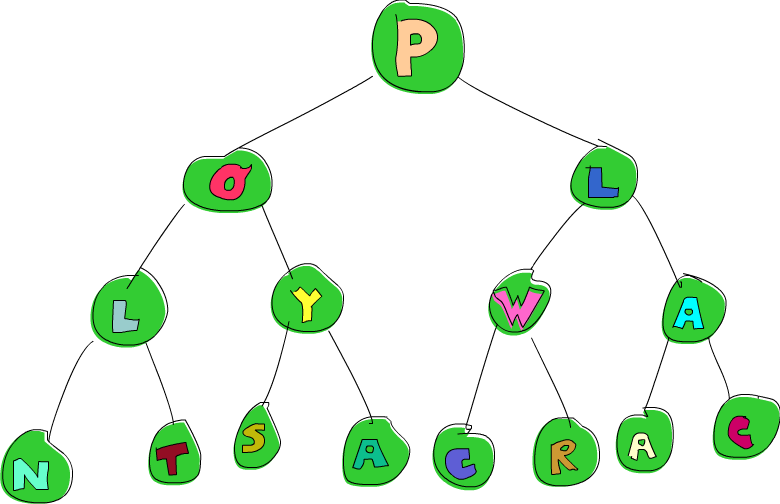
Notice that W in the tree there? Say we want to change it into a P. How would we go about doing that? Well, one way would be to pattern match on our tree until we find the element that's located by first going right and then left and changing said element. Here's the code for this:

changeToP :: Tree Char -> Tree Char
changeToP (Node x l (Node y (Node _ m n) r)) = Node x l (Node y (Node 'P' m n) r)

Yuck! Not only is this rather ugly, it's also kind of confusing. What happens here? Well, we pattern match on our tree and name its root element x (that's becomes the 'P' in the root) and its left subtree l. Instead of giving a name to its right subtree, we further pattern match on it. We continue this pattern matching until we reach the subtree whose root is our 'W'. Once we've done this, we rebuild the tree, only the subtree that contained the 'W' at its root now has a 'P'.

Is there a better way of doing this? How about we make our function take a tree along with a list of directions. The directions will be either L or R, representing left and right respectively, and we'll change the element that we arrive at if we follow the supplied directions. Here it is:

data Direction = L | R deriving (Show)
type Directions = [Direction]

changeToP :: Directions-> Tree Char -> Tree Char
changeToP (L:ds) (Node x l r) = Node x (changeToP ds l) r
changeToP (R:ds) (Node x l r) = Node x l (changeToP ds r)
changeToP [] (Node _ l r) = Node 'P' l r

If the first element in our list of directions is L, we construct a new tree that's like the old tree, only its left subtree has an element changed to 'P'. When we recursively call changeToP, we give it only the tail of the list of directions, because we already took a left. We do the same thing in the case of an R. If the list of directions is empty, that means that we're at our destination, so we return a tree that's like the one supplied, only it has 'P' as its root element.

To avoid printing out the whole tree, let's make a function that takes a list of directions and tells us what the element at the destination is:

elemAt :: Directions -> Tree a -> a
elemAt (L:ds) (Node _ l _) = elemAt ds l
elemAt (R:ds) (Node _ _ r) = elemAt ds r
elemAt [] (Node x _ _) = x

This function is actually quite similar to changeToP, only instead of remembering stuff along the way and reconstructing the tree, it ignores everything except its destination. Here we change the 'W' to a 'P' and see if the change in our new tree sticks:

ghci> let newTree = changeToP [R,L] freeTree
ghci> elemAt [R,L] newTree
'P'

Nice, this seems to work. In these functions, the list of directions acts as a sort of focus, because it pinpoints one exact subtree from our tree. A direction list of [R] focuses on the subtree that's right of the root, for example. An empty direction list focuses on the main tree itself.

While this technique may seem cool, it can be rather inefficient, especially if we want to repeatedly change elements. Say we have a really huge tree and a long direction list that points to some element all the way at the bottom of the tree. We use the direction list to take a walk along the tree and change an element at the bottom. If we want to change another element that's close to the element that we've just changed, we have to start from the root of the tree and walk all the way to the bottom again! What a drag.

In the next section, we'll find a better way of focusing on a subtree, one that allows us to efficiently switch focus to subtrees that are nearby.

A trail of breadcrumbs

Okay, so for focusing on a subtree, we want something better than just a list of directions that we always follow from the root of our tree. Would it help if we start at the root of the tree and move either left or right one step at a time and sort of leave breadcrumbs? That is, when we go left, we remember that we went left and when we go right, we remember that we went right. Sure, we can try that.

To represent our breadcrumbs, we'll also use a list of Direction (which is either L or R), only instead of calling it Directions, we'll call it Breadcrumbs , because our directions will now be reversed since we're leaving them as we go down our tree:

type Breadcrumbs = [Direction]

Here's a function that takes a tree and some breadcrumbs and moves to the left subtree while adding L to the head of the list that represents our breadcrumbs:

goLeft :: (Tree a, Breadcrumbs) -> (Tree a, Breadcrumbs)
goLeft (Node _ l _, bs) = (l, L:bs)

We ignore the element at the root and the right subtree and just return the left subtree along with the old breadcrumbs with L as the head. Here's a function to go right:

goRight :: (Tree a, Breadcrumbs) -> (Tree a, Breadcrumbs)
goRight (Node _ _ r, bs) = (r, R:bs)

It works the same way. Let's use these functions to take our freeTree and go right and then left:

ghci> goLeft (goRight (freeTree, []))
(Node 'W' (Node 'C' Empty Empty) (Node 'R' Empty Empty),[L,R])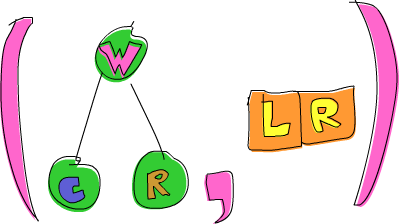

Okay, so now we have a tree that has 'W' in its root and 'C' in the root of its left subtree and 'R' in the root of its right subtree. The breadcrumbs are [L,R], because we first went right and then left.

To make walking along our tree clearer, we can use the -: function that we defined like so:

x -: f = f x

Which allows us to apply functions to values by first writing the value, then writing a -: and then the function. So instead of goRight (freeTree, []), we can write (freeTree, []) -: goRight. Using this, we can rewrite the above so that it's more apparent that we're first going right and then left:

ghci> (freeTree, []) -: goRight -: goLeft
(Node 'W' (Node 'C' Empty Empty) (Node 'R' Empty Empty),[L,R])

Going back up

What if we now want to go back up in our tree? From our breadcrumbs we know that the current tree is the left subtree of its parent and that it is the right subtree of its parent, but that's it. They don't tell us enough about the parent of the current subtree for us to be able to go up in the tree. It would seem that apart from the direction that we took, a single breadcrumb should also contain all other data that we need to go back up. In this case, that's the element in the parent tree along with its right subtree.

In general, a single breadcrumb should contain all the data needed to reconstruct the parent node. So it should have the information from all the paths that we didn't take and it should also know the direction that we did take, but it must not contain the subtree that we're currently focusing on. That's because we already have that subtree in the first component of the tuple, so if we also had it in the breadcrumbs, we'd have duplicate information.

Let's modify our breadcrumbs so that they also contain information about everything that we previously ignored when moving left and right. Instead of Direction, we'll make a new data type:

data Crumb a = LeftCrumb a (Tree a) | RightCrumb a (Tree a) deriving (Show)

Now, instead of just L, we have a LeftCrumb that also contains the element in the node that we moved from and the right tree that we didn't visit. Instead of R, we have RightCrumb, which contains the element in the node that we moved from and the left tree that we didn't visit.

These breadcrumbs now contain all the data needed to recreate the tree that we walked through. So instead of just being normal bread crumbs, they're now more like floppy disks that we leave as we go along, because they contain a lot more information than just the direction that we took.

In essence, every breadcrumb is now like a tree node with a hole in it. When we move deeper into a tree, the breadcrumb carries all the information that the node that we moved away from carried except the subtree that we chose to focus on. It also has to note where the hole is. In the case of a LeftCrumb, we know that we moved left, so the subtree that's missing is the left one.

Let's also change our Breadcrumbs type synonym to reflect this:

type Breadcrumbs a = [Crumb a]

Next up, we have to modify the goLeft and goRight functions to store information about the paths that we didn't take in our breadcrumbs, instead of ignoring that information like they did before. Here's goLeft:

goLeft :: (Tree a, Breadcrumbs a) -> (Tree a, Breadcrumbs a)
goLeft (Node x l r, bs) = (l, LeftCrumb x r:bs)

You can see that it's very similar to our previous goLeft, only instead of just adding a L to the head of our list of breadcrumbs, we add a LeftCrumb to signify that we went left and we equip our LeftCrumb with the element in the node that we moved from (that's the x) and the right subtree that we chose not to visit.

Note that this function assumes that the current tree that's under focus isn't Empty. An empty tree doesn't have any subtrees, so if we try to go left from an empty tree, an error will occur because the pattern match on Node won't succeed and there's no pattern that takes care of Empty.

goRight is similar:

goRight :: (Tree a, Breadcrumbs a) -> (Tree a, Breadcrumbs a)
goRight (Node x l r, bs) = (r, RightCrumb x l:bs)

We were previously able to go left and right. What we've gotten now is the ability to actually go back up by remembering stuff about the parent nodes and the paths that we didn't visit. Here's the goUp function:

goUp :: (Tree a, Breadcrumbs a) -> (Tree a, Breadcrumbs a)
goUp (t, LeftCrumb x r:bs) = (Node x t r, bs)
goUp (t, RightCrumb x l:bs) = (Node x l t, bs)

We're focusing on the tree t and we check what the latest Crumb is. If it's a LeftCrumb, then we construct a new tree where our tree t is the left subtree and we use the information about the right subtree that we didn't visit and the element to fill out the rest of the Node. Because we moved back so to speak and picked up the last breadcrumb to recreate with it the parent tree, the new list of breadcrumbs doesn't contain it.

Note that this function causes an error if we're already at the top of a tree and we want to move up. Later on, we'll use the Maybe monad to represent possible failure when moving focus.

With a pair of Tree a and Breadcrumbs a, we have all the information to rebuild the whole tree and we also have a focus on a subtree. This scheme also enables us to easily move up, left and right. Such a pair that contains a focused part of a data structure and its surroundings is called a zipper, because moving our focus up and down the data structure resembles the operation of a zipper on a regular pair of pants. So it's cool to make a type synonym as such:

type Zipper a = (Tree a, Breadcrumbs a)

I'd prefer naming the type synonym Focus because that makes it clearer that we're focusing on a part of a data structure, but the term zipper is more widely used to describe such a setup, so we'll stick with Zipper.

Manipulating trees under focus

Now that we can move up and down, let's make a function that modifies the element in the root of the subtree that the zipper is focusing on:

modify :: (a -> a) -> Zipper a -> Zipper a
modify f (Node x l r, bs) = (Node (f x) l r, bs)
modify f (Empty, bs) = (Empty, bs)

If we're focusing on a node, we modify its root element with the function f. If we're focusing on an empty tree, we leave it as it is. Now we can start off with a tree, move to anywhere we want and modify an element, all while keeping focus on that element so that we can easily move further up or down. An example:

ghci> let newFocus = modify (\_ -> 'P') (goRight (goLeft (freeTree,[])))

We go left, then right and then modify the root element by replacing it with a 'P'. This reads even better if we use -::

ghci> let newFocus = (freeTree,[]) -: goLeft -: goRight -: modify (\_ -> 'P')

We can then move up if we want and replace an element with a mysterious 'X':

ghci> let newFocus2 = modify (\_ -> 'X') (goUp newFocus)

Or if we wrote it with -::

ghci> let newFocus2 = newFocus -: goUp -: modify (\_ -> 'X')

Moving up is easy because the breadcrumbs that we leave form the part of the data structure that we're not focusing on, but it's inverted, sort of like turning a sock inside out. That's why when we want to move up, we don't have to start from the root and make our way down, but we just take the top of our inverted tree, thereby un-inverting a part of it and adding it to our focus.

Each node has two subtrees, even if those subtrees are empty trees. So if we're focusing on an empty subtree, one thing we can do is to replace it with a non-empty subtree, thus attaching a tree to a leaf node. The code for this is simple:

attach :: Tree a -> Zipper a -> Zipper a
attach t (_, bs) = (t, bs)

We take a tree and a zipper and return a new zipper that has its focus replaced with the supplied tree. Not only can we extend trees this way by replacing empty subtrees with new trees, we can also replace whole existing subtrees. Let's attach a tree to the far left of our freeTree:

ghci> let farLeft = (freeTree,[]) -: goLeft -: goLeft -: goLeft -: goLeft
ghci> let newFocus = farLeft -: attach (Node 'Z' Empty Empty)

newFocus is now focused on the tree that we just attached and the rest of the tree lies inverted in the breadcrumbs. If we were to use goUp to walk all the way to the top of the tree, it would be the same tree as freeTree but with an additional 'Z' on its far left.

I'm going straight to the top, oh yeah, up where the air is fresh and clean!

Making a function that walks all the way to the top of the tree, regardless of what we're focusing on, is really easy. Here it is:

topMost :: Zipper a -> Zipper a
topMost (t,[]) = (t,[])
topMost z = topMost (goUp z)

If our trail of beefed up breadcrumbs is empty, this means that we're already at the root of our tree, so we just return the current focus. Otherwise, we go up to get the focus of the parent node and then recursively apply topMost to that. So now we can walk around our tree, going left and right and up, applying modify and attach as we go along and then when we're done with our modifications, we use topMost to focus on the root of our tree and see the changes that we've done in proper perspective.

Focusing on lists

Zippers can be used with pretty much any data structure, so it's no surprise that they can be used to focus on sub-lists of lists. After all, lists are pretty much like trees, only where a node in a tree has an element (or not) and several subtrees, a node in a list has an element and only a single sub-list. When we implemented our own lists, we defined our data type like so:

data List a = Empty | Cons a (List a) deriving (Show, Read, Eq, Ord)

Contrast this with our definition of our binary tree and it's easy to see how lists can be viewed as trees where each node has only one subtree.

A list like [1,2,3] can be written as 1:2:3:[]. It consists of the head of the list, which is 1 and then the list's tail, which is 2:3:[]. In turn, 2:3:[] also has a head, which is 2 and a tail, which is 3:[]. With 3:[], the 3 is the head and the tail is the empty list [].

Let's make a zipper for lists. To change the focus on sub-lists of a list, we move either forward or back (whereas with trees we moved either up or left or right). The focused part will be a subtree and along with that we'll leave breadcrumbs as we move forward. Now what would a single breadcrumb for a list consist of? When we were dealing with binary trees, we said that a breadcrumb has to hold the element in the root of the parent node along with all the subtrees that we didn't choose. It also had to remember if we went left or right. So, it had to have all the information that a node has except for the subtree that we chose to focus on.

Lists are simpler than trees, so we don't have to remember if we went left or right, because there's only one way to go deeper into a list. Because there's only one subtree to each node, we don't have to remember the paths that we didn't take either. It seems that all we have to remember is the previous element. If we have a list like [3,4,5] and we know that the previous element was 2, we can go back by just putting that element at the head of our list, getting [2,3,4,5].

Because a single breadcrumb here is just the element, we don't really have to put it inside a data type, like we did when we made the Crumb data type for tree zippers:

type ListZipper a = ([a],[a])

The first list represents the list that we're focusing on and the second list is the list of breadcrumbs. Let's make functions that go forward and back into lists:

goForward :: ListZipper a -> ListZipper a
goForward (x:xs, bs) = (xs, x:bs)

goBack :: ListZipper a -> ListZipper a
goBack (xs, b:bs) = (b:xs, bs)

When we're going forward, we focus on the tail of the current list and leave the head element as a breadcrumb. When we're moving backwards, we take the latest breadcrumb and put it at the beginning of the list.

Here are these two functions in action:

ghci> let xs = [1,2,3,4]
ghci> goForward (xs,[])
([2,3,4],[1])
ghci> goForward ([2,3,4],[1])
([3,4],[2,1])
ghci> goForward ([3,4],[2,1])
([4],[3,2,1])
ghci> goBack ([4],[3,2,1])
([3,4],[2,1])

We see that the breadcrumbs in the case of lists are nothing more but a reversed part of our list. The element that we move away from always goes into the head of the breadcrumbs, so it's easy to move back by just taking that element from the head of the breadcrumbs and making it the head of our focus.

This also makes it easier to see why we call this a zipper, because this really looks like the slider of a zipper moving up and down.

If you were making a text editor, you could use a list of strings to represent the lines of text that are currently opened and you could then use a zipper so that you know which line the cursor is currently focused on. By using a zipper, it would also make it easier to insert new lines anywhere in the text or delete existing ones.

A very simple file system

Now that we know how zippers work, let's use trees to represent a very simple file system and then make a zipper for that file system, which will allow us to move between folders, just like we usually do when jumping around our file system.

If we take a simplistic view of the average hierarchical file system, we see that it's mostly made up of files and folders. Files are units of data and come with a name, whereas folders are used to organize those files and can contain files or other folders. So let's say that an item in a file system is either a file, which comes with a name and some data, or a folder, which has a name and then a bunch of items that are either files or folders themselves. Here's a data type for this and some type synonyms so we know what's what:

type Name = String
type Data = String
data FSItem = File Name Data | Folder Name [FSItem] deriving (Show)

A file comes with two strings, which represent its name and the data it holds. A folder comes with a string that is its name and a list of items. If that list is empty, then we have an empty folder.

Here's a folder with some files and sub-folders:

myDisk :: FSItem
myDisk =
    Folder "root"
        [ File "goat_yelling_like_man.wmv" "baaaaaa"
        , File "pope_time.avi" "god bless"
        , Folder "pics"
            [ File "ape_throwing_up.jpg" "bleargh"
            , File "watermelon_smash.gif" "smash!!"
            , File "skull_man(scary).bmp" "Yikes!"
            ]
        , File "dijon_poupon.doc" "best mustard"
        , Folder "programs"
            [ File "fartwizard.exe" "10gotofart"
            , File "owl_bandit.dmg" "mov eax, h00t"
            , File "not_a_virus.exe" "really not a virus"
            , Folder "source code"
                [ File "best_hs_prog.hs" "main = print (fix error)"
                , File "random.hs" "main = print 4"
                ]
            ]
        ]

That's actually what my disk contains right now.

A zipper for our file system

Now that we have a file system, all we need is a zipper so we can zip and zoom around it and add, modify and remove files as well as folders. Like with binary trees and lists, we're going to be leaving breadcrumbs that contain info about all the stuff that we chose not to visit. Like we said, a single breadcrumb should be kind of like a node, only it should contain everything except the subtree that we're currently focusing on. It should also note where the hole is so that once we move back up, we can plug our previous focus into the hole.

In this case, a breadcrumb should be like a folder, only it should be missing the folder that we currently chose. Why not like a file, you ask? Well, because once we're focusing on a file, we can't move deeper into the file system, so it doesn't make sense to leave a breadcrumb that says that we came from a file. A file is sort of like an empty tree.

If we're focusing on the folder "root" and we then focus on the file "dijon_poupon.doc", what should the breadcrumb that we leave look like? Well, it should contain the name of its parent folder along with the items that come before the file that we're focusing on and the items that come after it. So all we need is a Name and two lists of items. By keeping separate lists for the items that come before the item that we're focusing and for the items that come after it, we know exactly where to place it once we move back up. So this way, we know where the hole is.

Here's our breadcrumb type for the file system:

data FSCrumb = FSCrumb Name [FSItem] [FSItem] deriving (Show)

And here's a type synonym for our zipper:

type FSZipper = (FSItem, [FSCrumb])

Going back up in the hierarchy is very simple. We just take the latest breadcrumb and assemble a new focus from the current focus and breadcrumb. Like so:

fsUp :: FSZipper -> FSZipper
fsUp (item, FSCrumb name ls rs:bs) = (Folder name (ls ++ [item] ++ rs), bs)

Because our breadcrumb knew what the parent folder's name was, as well as the items that came before our focused item in the folder (that's ls) and the ones that came after (that's rs), moving up was easy.

How about going deeper into the file system? If we're in the "root" and we want to focus on "dijon_poupon.doc", the breadcrumb that we leave is going to include the name "root" along with the items that precede "dijon_poupon.doc" and the ones that come after it.

Here's a function that, given a name, focuses on a file of folder that's located in the current focused folder:

import Data.List (break)

fsTo :: Name -> FSZipper -> FSZipper
fsTo name (Folder folderName items, bs) =
    let (ls, item:rs) = break (nameIs name) items
    in  (item, FSCrumb folderName ls rs:bs)

nameIs :: Name -> FSItem -> Bool
nameIs name (Folder folderName _) = name == folderName
nameIs name (File fileName _) = name == fileName

fsTo takes a Name and a FSZipper and returns a new FSZipper that focuses on the file with the given name. That file has to be in the current focused folder. This function doesn't search all over the place, it just looks at the current folder.

First we use break to break the list of items in a folder into those that precede the file that we're searching for and those that come after it. If you remember, break takes a predicate and a list and returns a pair of lists. The first list in the pair holds items for which the predicate returns False. Then, once the predicate returns True for an item, it places that item and the rest of the list in the second item of the pair. We made an auxiliary function called nameIs that takes a name and a file system item and returns True if the names match.

So now, ls is a list that contains the items that precede the item that we're searching for, item is that very item and rs is the list of items that come after it in its folder. Now that we have this, we just present the item that we got from break as the focus and build a breadcrumb that has all the data it needs.

Note that if the name we're looking for isn't in the folder, the pattern item:rs will try to match on an empty list and we'll get an error. Also, if our current focus isn't a folder at all but a file, we get an error as well and the program crashes.

Now we can move up and down our file system. Let's start at the root and walk to the file "skull_man(scary).bmp":

ghci> let newFocus = (myDisk,[]) -: fsTo "pics" -: fsTo "skull_man(scary).bmp"

newFocus is now a zipper that's focused on the "skull_man(scary).bmp" file. Let's get the first component of the zipper (the focus itself) and see if that's really true:

ghci> fst newFocus
File "skull_man(scary).bmp" "Yikes!"

Let's move up and then focus on its neighboring file "watermelon_smash.gif":

ghci> let newFocus2 = newFocus -: fsUp -: fsTo "watermelon_smash.gif"
ghci> fst newFocus2
File "watermelon_smash.gif" "smash!!"

Manipulating our file system

Now that we know how to navigate our file system, manipulating it is easy. Here's a function that renames the currently focused file or folder:

fsRename :: Name -> FSZipper -> FSZipper
fsRename newName (Folder name items, bs) = (Folder newName items, bs)
fsRename newName (File name dat, bs) = (File newName dat, bs)

Now we can rename our "pics" folder to "cspi":

ghci> let newFocus = (myDisk,[]) -: fsTo "pics" -: fsRename "cspi" -: fsUp

We descended to the "pics" folder, renamed it and then moved back up.

How about a function that makes a new item in the current folder? Behold:

fsNewFile :: FSItem -> FSZipper -> FSZipper
fsNewFile item (Folder folderName items, bs) =
    (Folder folderName (item:items), bs)

Easy as pie. Note that this would crash if we tried to add an item but weren't focusing on a folder, but were focusing on a file instead.

Let's add a file to our "pics" folder and then move back up to the root:

ghci> let newFocus = (myDisk,[]) -: fsTo "pics" -: fsNewFile (File "heh.jpg" "lol") -: fsUp

What's really cool about all this is that when we modify our file system, it doesn't actually modify it in place but it returns a whole new file system. That way, we have access to our old file system (in this case, myDisk) as well as the new one (the first component of newFocus). So by using zippers, we get versioning for free, meaning that we can always refer to older versions of data structures even after we've changed them, so to speak. This isn't unique to zippers, but is a property of Haskell because its data structures are immutable. With zippers however, we get the ability to easily and efficiently walk around our data structures, so the persistence of Haskell's data structures really begins to shine.

Watch your step

So far, while walking through our data structures, whether they were binary trees, lists or file systems, we didn't really care if we took a step too far and fell off. For instance, our goLeft function takes a zipper of a binary tree and moves the focus to its left subtree:

goLeft :: Zipper a -> Zipper a
goLeft (Node x l r, bs) = (l, LeftCrumb x r:bs)

But what if the tree we're stepping off from is an empty tree? That is, what if it's not a Node, but an Empty? In this case, we'd get a runtime error because the pattern match would fail and we have made no pattern to handle an empty tree, which doesn't have any subtrees at all. So far, we just assumed that we'd never try to focus on the left subtree of an empty tree as its left subtree doesn't exist at all. But going to the left subtree of an empty tree doesn't make much sense, and so far we've just conveniently ignored this.

Or what if we were already at the root of some tree and didn't have any breadcrumbs but still tried to move up? The same thing would happen. It seems that when using zippers, any step could be our last (cue ominous music). In other words, any move can result in a success, but it can also result in a failure. Does that remind you of something? Of course, monads! More specifically, the Maybe monad which adds a context of possible failure to normal values.

So let's use the Maybe monad to add a context of possible failure to our movements. We're going to take the functions that work on our binary tree zipper and we're going to make them into monadic functions. First, let's take care of possible failure in goLeft and goRight. So far, the failure of functions that could fail was always reflected in their result, and this time is no different. So here are goLeft and goRight with an added possibility of failure:

goLeft :: Zipper a -> Maybe (Zipper a)
goLeft (Node x l r, bs) = Just (l, LeftCrumb x r:bs)
goLeft (Empty, _) = Nothing

goRight :: Zipper a -> Maybe (Zipper a)
goRight (Node x l r, bs) = Just (r, RightCrumb x l:bs)
goRight (Empty, _) = Nothing

Cool, now if we try to take a step to the left of an empty tree, we get a Nothing!

ghci> goLeft (Empty, [])
Nothing
ghci> goLeft (Node 'A' Empty Empty, [])
Just (Empty,[LeftCrumb 'A' Empty])

Looks good! How about going up? The problem before happened if we tried to go up but we didn't have any more breadcrumbs, which meant that we were already in the root of the tree. This is the goUp function that throws an error if we don't keep within the bounds of our tree:

goUp :: Zipper a -> Zipper a
goUp (t, LeftCrumb x r:bs) = (Node x t r, bs)
goUp (t, RightCrumb x l:bs) = (Node x l t, bs)

Now let's modify it to fail gracefully:

goUp :: Zipper a -> Maybe (Zipper a)
goUp (t, LeftCrumb x r:bs) = Just (Node x t r, bs)
goUp (t, RightCrumb x l:bs) = Just (Node x l t, bs)
goUp (_, []) = Nothing

If we have breadcrumbs, everything is okay and we return a successful new focus, but if we don't, then we return a failure.

Before, these functions took zippers and returned zippers, which meant that we could chain them like this to walk around:

gchi> let newFocus = (freeTree,[]) -: goLeft -: goRight

But now, instead of returning Zipper a, they return Maybe (Zipper a), so chaining functions like this won't work. We had a similar problem when we were dealing with our tightrope walker in the chapter about monads. He also walked one step at a time and each of his steps could result in failure because a bunch of birds could land on one side of his balancing pole and make him fall.

Now, the joke's on us because we're the ones doing the walking, and we're traversing a labyrinth of our own devising. Luckily, we can learn from the tightrope walker and just do what he did, which is to exchange normal function application for using >>=, which takes a value with a context (in our case, the Maybe (Zipper a), which has a context of possible failure) and feeds it into a function while making sure that the context is taken care of. So just like our tightrope walker, we're going to trade in all our -: operators for >>=. Alright, we can chain our functions again! Watch:

ghci> let coolTree = Node 1 Empty (Node 3 Empty Empty)
ghci> return (coolTree,[]) >>= goRight
Just (Node 3 Empty Empty,[RightCrumb 1 Empty])
ghci> return (coolTree,[]) >>= goRight >>= goRight
Just (Empty,[RightCrumb 3 Empty,RightCrumb 1 Empty])
ghci> return (coolTree,[]) >>= goRight >>= goRight >>= goRight
Nothing

We used return to put a zipper in a Just and then used >>= to feed that to our goRight function. First, we made a tree that has on its left an empty subtree and on its right a node that has two empty subtrees. When we try to go right once, the result is a success, because the operation makes sense. Going right twice is okay too; we end up with the focus on an empty subtree. But going right three times wouldn't make sense, because we can't go to the right of an empty subtree, which is why the result is a Nothing.

Now we've equipped our trees with a safety-net that will catch us should we fall off. Wow, I nailed this metaphor.

Our file system also has a lot of cases where an operation could fail, such as trying to focus on a file or folder that doesn't exist. As an exercise, you can equip our file system with functions that fail gracefully by using the Maybe monad.